本試卷分選擇題和非選擇題兩部分.滿分l50分，考試時(shí)間l20分鐘.

　　選擇題

　　一、選擇題：本大題共l7小題，每小題5分，共85分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

　　(1)已知集合A={1，2，3，4，6，12}，C={1，2，3，6，9，18}，則A∩C=

　　A.{1，2，3，4，6，9，12，18}

　　B.{1,2，3，6}

　　C.{1，3，6}

　　D.{1，2，6}

　　(2)(1+i)4的值是(成人高考更多完整資料免費(fèi)提供加微信/QQ：29838818)

　　A.2 B.2i C.4 D.-4

(3)

　　A.-2 B.-1 C.0 D.1

　　(4)若向量a=(1，2)，b=(-3，4)，則(a·b)(a+b)等于

　　A.20 B.(-10，30) C.54 D.(-8，24)

　　(5)棱長為a的正方體，其外接球的表面積為

　　A.πa2B.4πa2C.3πa2D.12πa2

　　(6)三角形全等是三角形面積相等的

　　A.充分但不必要條件 B.必要但不充分條件

　　C.充要條件 D.既不充分也不必要條件

　　(7)已知y=f(x)(x∈R)是以4為周期的奇函數(shù)，且f(l)=1,f(3)=a，則有

　　A.a=1 B.a=2 C.a=-1 D.a=-2

　　(8)等差數(shù)列{an}的公差d<0，且n2·n4=12，a2+a4=8，則數(shù)列{an}的通項(xiàng)公式是

　　A.an=2n-2(n∈N*)B.an=2n+4(n∈N*)

　　C.an=-2n+12(n∈N*) D.an=-2n+10(n∈N*)

　　(9)方程2x2-5x+2=0的兩根可分別作為

　　A.一個(gè)橢圓和一個(gè)雙曲線的離心率 B.兩個(gè)拋物線的離心率

　　C.一個(gè)橢圓和一個(gè)拋物線的離心率 D.兩個(gè)橢圓的離心率

　　(10)甲、乙兩人獨(dú)立地解同一個(gè)問題，甲解決這個(gè)問題的概率是P1，乙解決這個(gè)問題的概率是P2，那么其中至少有1人解決這個(gè)問題的概率是

　　A.P1+P2B.P1P2C.1-P1P2D.1-(1-P1)(1一P2)

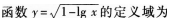
(11)

　　A.{x|x>0} B.{x|0

　　(12)5個(gè)人排成一排，甲、乙相鄰的不同排法有

　　A.60種 B.48種 C.36種 D.24種

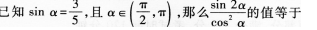
(13)

　　(14)拋物線y=ax2的準(zhǔn)線方程是y=2，則a的值為

　　(15)一名同學(xué)投籃的命中率為2/3，他連續(xù)投籃3次，其中恰有2次命中的概率p為

　　(16)直線Y=ax+2與直線Y=3x-b關(guān)于直線y=x對(duì)稱，則

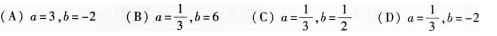
　　(17)函數(shù)Y=1+3x-x3有

　　A.極小值-1，極大值1 B.極小值-2，極大值3

　　C.極小值-2，極大值2 D.極小值-1，極大值3

非選擇題

　　二、填空題：本大題共4小題，每小題4分，共l6分.把答案填在題中橫線上.

(18)(成人高考更多完整資料免費(fèi)提供加微信/QQ：29838818)

　　(19)設(shè)(x+2)4=a0x4+a1x3+a2x2+a3x+a4,則a4=____.

　　(20)函數(shù)y=4sin xcosx的最小正周期及最大值分別是____.

　　(21)曲線y=2x2-1在點(diǎn)(1，1)處的切線方程是___.

　　三、解答題：本大題共4小題，共49分.解答應(yīng)寫出推理、演算步驟.

　　(22)(本小題滿分l2分)

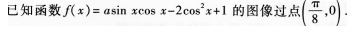
　　(I)求實(shí)數(shù)a的值;

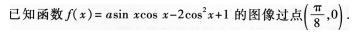
(II)

　　(23)(本小題滿分12分)

　　已知等差數(shù)列{an}中，a1=9，a3+a8=0.

　　(I)求數(shù)列{an}的通項(xiàng)公式;

　　(Ⅱ)當(dāng)n為何值時(shí)，數(shù)列{an}的前n項(xiàng)和Sn取得最大值，并求該最大值.

　　(24)(本小題滿分12分)

　　已知拋物線C：x2=2py(p>O)的焦點(diǎn)F在直線l:x-y+1=0上.

　　(I)求拋物線C的方程;

　　(Ⅱ)設(shè)直線f與拋物線C相交于P，Q兩點(diǎn)，求線段PQ中點(diǎn)M的坐標(biāo).

　　(25)(本小題滿分l3分)

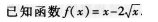
　　(I)求函數(shù)y=f(x)的單調(diào)區(qū)間，并指出它在各單調(diào)區(qū)間上是增函數(shù)還是減函數(shù);

　　(Ⅱ)求函數(shù)y=f(x)在區(qū)間[0，4]上的最大值和最小值.

　　答案解析

　　一、選擇題

　　(1)【參考答案】 (B)

　　集合A∩C是由同時(shí)屬于集合A和集合C的元素組成的集合，易得答案為A∩C={1，2，3,6}.

　　【解題指要】本題考查集合的運(yùn)算.注意A∪C的結(jié)果是(A)，二者是不同的.

　　(2)【參考答案】 (D)

　　(1+i)4=[(1+i)2]2=(2i)2=-4.

　　【解題指要】本題考杏復(fù)數(shù)運(yùn)算.在復(fù)數(shù)運(yùn)算中，要記住：

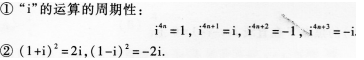
　　(3)【參考答案】 (A)

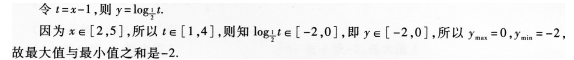
　　【解題指要】本題考查函數(shù)值域的求法，一般采用直接法求解.

　　(4)【參考答案】 (B)

　　(a·b)(a+b)=[(1，2)·(-3，4)][(1，2)+(-3，4)] =(-3+8)(-2，6)=5(-2，6)=(-l0，30).

　　【解題指要】本題考查向量的運(yùn)算.向量數(shù)量積的結(jié)果是實(shí)數(shù)，向量和數(shù)的乘積的結(jié)果是

　　向量.

　　(5)【參考答案】 (C)

　　【解題指要】本題考查正方體和球的相關(guān)知識(shí).

　　(6)【參考答案】 (A)

　　若兩個(gè)三角形全等，則它們的面積相等;然而，面積相等的三角形卻不一定是全等三角形，因此答案為充分但不必要條件，選(A).

　　【解題指要】本題考查充分必要條件的相關(guān)知識(shí).

　　(7)【參考答案】 (C)

　　因?yàn)閒(x)是以4為周期的奇函數(shù)，所以

　　f(3)=f(3-4)=f(-l)=-f(1)，

　　即a=-f(1).

　　又f(1)=1，所以a=-1.

　　【解題指要】本題考查函數(shù)的奇偶性和周期性.

　　(8)【參考答案】 (D)

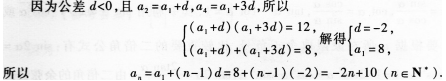
　　【解題指要】本題考查等差數(shù)列的通項(xiàng)公式.

　　(9)【參考答案】(A)

　　【解題指要】本題考查離心率的相關(guān)知識(shí).橢圓離心率的取值范圍是(0，1)，雙曲線離心率的取值范圍是(1，+∞)，拋物線的離心率為1.

　　(10)【參考答案】 (D)

　　【解題指要】本題考查獨(dú)立事件同時(shí)發(fā)生的概率.甲不能解決問題的概率為1-P1，乙不能解決問題的概率為1-p2，因此，兩人都不能獨(dú)立解決問題的概率為(1-p1)(1-p2)，從而其中至少有1人解決這個(gè)問題的概率為1-(1-p1)(1-p2).

　　(11)【參考答案】 (B)

　　二次根式要有意義，應(yīng)有1-lg x≥0，即lg x≤1=lg 10，所以0

　　【解題指要】本題考查二次根式的概念和對(duì)數(shù)函數(shù)的單調(diào)性，求解時(shí)要注意對(duì)數(shù)函數(shù)的定

　　義域.

　　(12)【參考答案】 (B)

　　【解題指要】本題考查排列組合的相關(guān)知識(shí).對(duì)于相鄰問題，采用捆綁法比較方便求解.

　　(13)【參考答案】 (B)

　　(14)【參考答案】 (B)

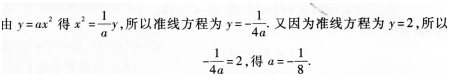
　　【解題指要】本題考查拋物線的標(biāo)準(zhǔn)方程及其相關(guān)幾何性質(zhì).拋物線的標(biāo)準(zhǔn)方程形式：二

　　幾何性質(zhì).

　　(15)【參考答案】 (D)

　　【解題指要】本題考查n次獨(dú)立重復(fù)事件概率的計(jì)算方法.

　　(16)【參考答案】 (B)

　　【解題指要】本題考查反函數(shù)的求法.求反函數(shù)要先“倒”：即把x用y表示;然后“換”：即

　　x換成y，y換成x;最后“注”：注明反函數(shù)的定義域(即原函數(shù)的值域).

　　(17)【參考答案】 (D)

　　由于y’=3-3x2，x=±1時(shí),y’=0，且x<-1時(shí)，y’<0;-1

　　【解題指要】本題考查導(dǎo)數(shù)的應(yīng)用.注意導(dǎo)數(shù)值為0的點(diǎn)，需它的“左鄰”和。“右鄰”的導(dǎo)數(shù)異號(hào).才能判斷其為極值點(diǎn)，若兩側(cè)導(dǎo)數(shù)同號(hào)則不行.例如y=x3，y'=3x2，當(dāng)x=0時(shí).雖然y'=0.但是x>0時(shí)y’>0，x

　　二、填空題

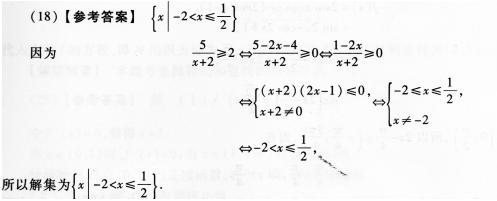
　　【解題指要】本題考查分式不等式的解法，其基本步驟如下：①移項(xiàng);②通分;③轉(zhuǎn)化為

　　整式不等式.

　　求解本題時(shí)要注意分母不為0這一條件.

　　(19)【參考答案】 l6

　　根據(jù)二項(xiàng)式定理，可知a4=24=16.【解題指要】 本題考查二項(xiàng)式定理.

　　(20)【參考答案】 π，2

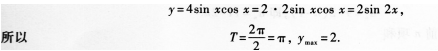
　　【解題指要】本題考查二倍角的正弦公式、三角函數(shù)的周期與最值等知識(shí).

　　(21)【參考答案】4x-Y-3=0

　　【解題指要】本題考查二倍角的正弦公式和余弦公式，考查兩角差的三角函數(shù)公式.本題

　　(23)【參考答案】

　　解(I)設(shè)等差數(shù)列{an}的公差為d，由已知a3+a8=0，得2a1+9d=0.又已知a1=9，所以d=-2.

　　數(shù)列{an}的通項(xiàng)公式為

　　an=9-2(n一l)，即an=11-2n.

　　(Ⅱ)數(shù)列{an}的前n項(xiàng)和

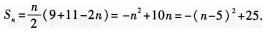
　　當(dāng)n=5時(shí)，Sn取得最大值25.

　　也可采用下面的方法：因?yàn)樵摰炔顢?shù)列遞減，要求其前n項(xiàng)和的最大值，只需關(guān)注該數(shù)列的

　　正項(xiàng)即可.令an=11-2n>0，得n<11/2，即取n為5.

　　易知數(shù)列的前5項(xiàng)依次為：9，7，5，3，1，故前n項(xiàng)和的最大值為

　　S5=9+7+5+3+1=25.

　　此法也是常見思路之一.

　　【解題指要】本題考查等差數(shù)列的通項(xiàng)公式和前n項(xiàng)和公式.

　　(24)【參考答案】

　　解(I)由拋物線方程x2=2py(p>0)為標(biāo)準(zhǔn)方程，知其焦點(diǎn)在y軸正半軸上.在直線x-y+1=0中，令x=0，得焦點(diǎn)坐標(biāo)為F(0，1)，所以p/2=1，即P=2，故拋物線C的方程是x2=4y.

　　(Ⅱ)設(shè)P，Q的坐標(biāo)分別為(x1，y1)，(x2，y2).

　　代入直線l的方程，得M的縱坐標(biāo)為yM=3，所以線段PQ中點(diǎn)M的坐標(biāo)為(2，3).

　　【解題指要】本題考查拋物線和直線的相關(guān)知識(shí).

　　【解題指要】本題考查導(dǎo)數(shù)的應(yīng)用：用導(dǎo)數(shù)判斷函數(shù)的單調(diào)區(qū)間和求函數(shù)的最大值、最小值.